skoot.balance.smote_balance¶
-
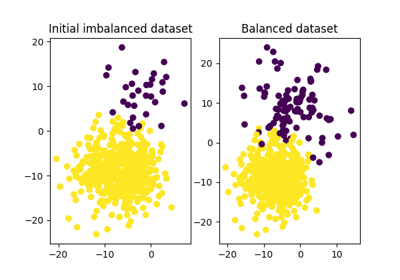
skoot.balance.smote_balance(X, y, return_estimators=False, balance_ratio=0.2, strategy='perturb', n_neighbors=5, algorithm='kd_tree', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=1, random_state=None, shuffle=True)[source][source]¶ Balance a dataset using SMOTE.
Synthetic Minority Oversampling TEchnique (SMOTE) is a class balancing strategy that samples the k-Nearest Neighbors from each minority class, perturbs them with a random value between 0 and 1, and adds the difference between the original observation and the perturbation to the original observation to generate a synthetic observation. This is repeated until the minority classes are represented at a prescribed ratio to the majority class.
Alternative methods involve interpolating the distance between the original observation and the nearest neighbors using either the median or the mean. This strategy can be set using the
strategyarg (one of ‘perturb’ or ‘interpolate’).Parameters: X : array-like, shape (n_samples, n_features)
The training array. Samples from the minority class(es) in this array will be interpolated until they are represented at
balance_ratio.y : array-like, shape (n_samples,)
Training labels corresponding to the samples in
X.return_estimators : bool, optional (default=False)
Whether or not to return the dictionary of fit :class:
sklearn.neighbors.NearestNeighborsinstances. If True, the return value will be a tuple, with the first index being the balancedXmatrix, the second index being theyvalues, and the third index being a dictionary of the fit estimators. If False, the return value is simply a tuple of the balancedXmatrix and the corresponding labels.balance_ratio : float, optional (default=0.2)
The minimum acceptable ratio of
$MINORITY_CLASS : $MAJORITY_CLASSrepresentation, where 0 <ratio<= 1strategy : str, optional (default=’perturb’)
The strategy used to construct synthetic examples from existing examples. The original SMOTE paper suggests a strategy by which a random value between 0 and 1 scales the difference between the nearest neighbors, and the difference is then added to the original vector. This is the default strategy, ‘perturb’. Valid strategies include:
- ‘perturb’ - a random value between 0 and 1 scales the difference
- between the nearest neighbors, and the difference is then added to the original vector.
- ‘interpolate’ - the
interpolation_method(‘mean’ or ‘median’) of the nearest neighbors constitutes the synthetic example.
n_neighbors : int, optional (default=5)
Number of neighbors to use by default for
kneighborsqueries. This parameter is passed to each respectiveNearestNeighbors call.algorithm : str or unicode, optional (default=’kd_tree’)
Algorithm used to compute the nearest neighbors. One of {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}:
- ‘ball_tree’ will use
sklearn.neighbors.BallTree - ‘kd_tree’ will use
sklearn.neighbors.KDtree - ‘brute’ will use a brute-force search.
- ‘auto’ will attempt to decide the most appropriate algorithm
based on the values passed to
fitmethod.
Note: fitting on sparse input will override the setting of this parameter, using brute force. This parameter is passed to each respective
NearestNeighborscall.leaf_size : int, optional (default=30)
Leaf size passed to
BallTreeorKDTree. This can affect the speed of the construction and query, as well as the memory required to store the tree. The optimal value depends on the nature of the problem.p : integer, optional (default=2)
Parameter for the Minkowski metric from
sklearn.metrics.pairwise.pairwise_distances. When p = 1, this is equivalent to using manhattan_distance (l1), and euclidean_distance (l2) for p = 2. For arbitrary p, minkowski_distance (l_p) is used.metric : string or callable, optional (default=’minkowski’)
Metric to use for distance computation. Any metric from scikit-learn or
scipy.spatial.distancecan be used.If metric is a callable function, it is called on each pair of instances (rows) and the resulting value recorded. The callable should take two arrays as input and return one value indicating the distance between them. This works for Scipy’s metrics, but is less efficient than passing the metric name as a string. Distance matrices are not supported.
Valid values for metric are:
- from scikit-learn: [‘cityblock’, ‘cosine’, ‘euclidean’, ‘l1’, ‘l2’, ‘manhattan’]
- from
scipy.spatial.distance: [‘braycurtis’, ‘canberra’, ‘chebyshev’, ‘correlation’, ‘dice’, ‘hamming’, ‘jaccard’, ‘kulsinski’, ‘mahalanobis’, ‘matching’, ‘minkowski’, ‘rogerstanimoto’, ‘russellrao’, ‘seuclidean’, ‘sokalmichener’, ‘sokalsneath’, ‘sqeuclidean’, ‘yule’]
See the documentation for
scipy.spatial.distancefor details on these metrics.metric_params : dict, optional (default = None)
Additional keyword arguments for the metric function.
n_jobs : int, optional (default = 1)
The number of parallel jobs to run for neighbors search. If
-1, then the number of jobs is set to the number of CPU cores. Affects onlykneighborsandkneighbors_graphmethods.shuffle : bool, optional (default=True)
Whether to shuffle the output.
random_state : int or None, optional (default=None)
The seed to construct the random state to generate random selections.
References
[R10] N. Chawla, K. Bowyer, L. Hall, W. Kegelmeyer, “SMOTE: Synthetic Minority Over-sampling Technique” https://www.jair.org/media/953/live-953-2037-jair.pdf Examples
>>> from sklearn.datasets import make_classification >>> X, y = make_classification(n_samples=1000, random_state=42, ... n_classes=2, weights=[0.99, 0.01]) >>> X_bal, y_bal = smote_balance(X, y, balance_ratio=0.2, random_state=42) >>> ratio = round((y_bal == 1).sum() / float((y_bal == 0).sum()), 1) >>> assert ratio == 0.2, ratio
Note that the count of samples is now greater than it initially was:
>>> assert X_bal.shape[0] > 1000